LA, LLNL, and Supercomputing
The Influence of the Los Alamos and Livermore National Laboratories on the Development of Supercomputing by Mackenzie (1991)
http://dx.doi.org/10.1109/MAHC.1991.10014
を読みながらのメモ。以下、論文からの引用とコメント:
The failure of suppliers to produce the required integrated circuits, anti-war demonstrations, riots, and fire bombing on the campus of the University of Illinois in 1970, and a range of other circumstances prevented the smooth development of ILLIAC IV.
ILLIAC IVについて。
The requisite calculations for one time-step for one cell might amount to 200 floating-point operations for the early 1960’s code, and 20,000 for the modern one (Livermore interviews).
核兵器のモデリングに必要な演算量について。この間に、モデルに利用されるメッシュも、2次元モデルから3次元モデルが必要になり、大幅に増加している。
Statically, up to 30% of the instructions in a Monte Carlo program may be branches (Michael interview).
メッシュ上で偏微分方程式の解を求める手法は、コードに分岐が少ないのに対して、核兵器モデリングでもうひとつ重要な計算手法であるモンテカルロ法は、本質的に分岐が多い。
One million IBM cards carried the requisite initial values, one card for each point in the computational mesh, and “the computations to be performed required the punching of intermediate output cards which were then resubmitted as input” (Stern 1981).
Los AlamosのFrankelとMetropolisが、最初にENIACで計算をしたモデルのこと。
Neither laboratory has bought one of the Japanese supercomputers, though here questions of nationalist protectionism come into play as well as the questions of the suitability of particular machines for the laboratories’ computational tasks.
Los AlamosとLivermoreは、スパコンの選択にうるさい。速いモデルだからという理由だけで計算機を選ぶことはなかった。当然、日本製のベクトルスパコンは選択されなかった。
The Control Data STAR-100 episode was pivotal, because it secured the commitment of the laboratories to mainstream supercomputing rather than the more massively parallel alternatives.
STAR-100というある意味画期的な計算機は、仕様を満たすことができなかったため、その後LAやLLNLはいわゆる普通の計算機(CDC Cyber205などのベクトル計算機)に強くコミットすることになった。実はこれらの核関連の研究は多くが機密であったため、本当に必要な「核」の部分のコードが公開されず、それをターゲットとしてのアーキテクチャやソフトの最適化が不可能という問題もあったようだ。そのため、LLNLではLivermore Loopsと呼ばれる、LLNLが必要としている計算の典型的なものを代表するベンチマークを用意するようになった。その後、色々な計算機はこの「ベンチマーク」の性能を競う風潮ができた。
The project was formulated in an “almost pathological atmosphere of optimism and its corollary, fear of being left behind” (Bashe et al. 1986); as outlined above, the designers were also trying to satisfy the needs of quite different kinds of users.
IBMのStretchについて。結果としてStretchは735個の命令をもつ計算機になってしまった。この直前に「VAXのアーキテクチャはDEC社内の官僚主義的な構造を反映している」というTom Westの言葉を、"The Soul of a New Machine"から引用している。IBMも同様の問題を抱えていたのだろう。
Livermore’s “Sidney Fernbach was reportedly one of the few people in the world from whom Seymour Cray would accept suggestions” (Lundstrom 1987, p. 90), and Cray took, and takes, care to become aware of the laboratories’ computational needs.
Cray-1は、LAやLLNLの要求にもとづいて設計された計算機ではなかった。実際、Crayは彼らのような核関連の研究だけでなく、NSAが必要としている計算にも配慮して、ある種のバランスのとれたアーキテクチャを開発することができて、そして成功した(Cray-1では)。それでも、この引用にあるように、LLNLによるCrayに対する影響が全くなかったわけではないらしい。"one of the few people"ねぇ。
Seymour Crayとスパコン
The social limits of speed: development and use of supercomputers" by Elzen & Mackenzie (1994)
http://dx.doi.org/10.1109/85.251854
を読みながらのメモ。以下、論文からの引用とコメント:
As one of Cray's famous maxims has it, he likes to start the design of a new-generation machine with "a clean sheet of paper."
CDC6600の成功後、次の計算機の設計方針についてのCrayの見解。Crayは過去のアーキテクチャとの互換は最重要視していなかった。結果的に、CrayはCDCの方針に反対し、CDCを退社してCRIを設立した。
Cray used to say that he knew all his users by their first names.
Crayは常に利用者(この場合アメリカの国立研究所の核関連の研究者達)のことを第一に考えて計算機を設計したらしい。
This was recognized even by IBM, prompting a famous acerbic memo to his staff from chairman Thomas J. Watson, Jr., inquiring why Cray's team of "34 people -- including the janitor" had outperformed the computing industry's mightiest corporation.
CDC6600が発売されたあとの当時のIBMのトップのメモ。"janitor"は守衛。
In 1980, it was unclear that the 200 kilowatts that were generated in such a small and densely packed computer could be dissipated.
3D基板で実装されたCray-2をどう冷却するのかという問題。結局フッ化炭素(液体)を使って冷却することになった。
In a sense, CRI gradually became the "prisoner of its own success." New innovations were constrained by the very socio-technical network that made CRI so successful.
これがこの論文の核心だろう。元々、CRIは、CrayがCDCの開発方針を受け入れることができず独立して設立した会社で、その目的はCrayの好きなように世界最速の計算機を作ることだった。Cray-1はそのもくろみ通りに、当時の世界最高速を実現した。一方でCRIは売り上げを伸ばすために、伝統的な顧客であった国立研究所以外にも、民間の会社への営業をするようになった。このときに"Hero-problems"という、その業界で重要な問題だが時間がかりすぎる問題を、CRIなら自社の計算機を使って高速化できる、というのを売りとして営業をした。色々と曲折はあったが、この戦略は成功し、民間のいろいろな大企業がCRIの計算機を導入した。その結果、それらの新しい顧客は必ずしも世界最速の計算機を求めているのではなく、ソフトウエア資産が継続的に利用可能かどうかや計算機の信頼性に重きをおいたため、CRIは、新しい世代の計算機のたびにアーキテクチャを一新するという、創業者のCray的なやりかたをとることが不可能になった。つまり、CRIは顧客の要望に基づいてハードとソフトを開発するようになったために、顧客はCRIのシステムに依存し、CRIはその呪縛から逃れることが不可能になった。これが90年代前半の状況。
"socio-technical network"とは、Crayとそのスパコンの利用者たちの関係性という意味での人間関係のつながりの意味と、上に書いたようなCRIの計算機とその顧客たちのとの強い関係性、さらにその影響下にある計算機のアーキテクチャやそのためのソフトウエア(OSやコンパイラ、ライブラリ、アプリまで)などの技術的な関係性、以上を総称した概念。技術的に世界最高速を目指すという、古き良きCrayら開拓者たちによるラディカルな計算機開発の時代は、技術的ではない制約を受けるようになり、1980年代の終わり頃には終焉しつつあった。それらの制約を避けて、新たな計算機を開発するには、CrayやSteve Chen(Cray Y-MPのアーキテクト)のように、CRIを退職して再び自分の会社を立ち上げるしかない。しかし、それが成功するかは別問題で、実際その二人の新しい計算機は失敗している。
Computerの前にScienceとEngineeringの教育を
すでに半年も前のワークショップだが、スライドが公開されていたので、いまさらながら閲覧してみた。
2011 Workshop on Achitechtures I: Exasclae and Beyond http://www.orau.gov/archI2011/
一通りみてみたが、内輪ネタがひどい(Murphy)のもあるし、ほとんど会社の技術的な宣伝しか書いてない(Borkar)のもあるし、スライドだけでは意味不明(Sterling)なものもあるし、色々。
Geistのスライドは"Resilience"をキーワードとして、exascale時代には今よりすべての部分(ハードもソフトも)でエラー率が桁で悪くなるので、どうすればよいかという話。ハード的に対応するのはもう不可能な時代であるから、また、OSやランタイムでどうにかするのもほとんど無理であるから、そもそものアルゴリズムをエラー前提で作る必要があるのでは、という提案。それとともに、大規模な並列計算機のシミュレーションをするためのソフトを作っている。プログラムのバグは再現できるから修正できるわけで、そもそも色々な「エラー」は再現することが困難であるからその場での対応はできず、せいぜいそれを検知して間違える前に戻ってやり直すというのが安直な解決策(checkpointing)ではある。しかし、今より大規模になるとcheckpointingをすることは事実上不可能になるので、エラー前提アルゴリズムを検討するために、アーキテクチャや計算機のシミュレーションが必要だということ。
Resnick("Within and Above the Exascale Program"のほう)の8ページにはぐうの音も出ない正論が。
Co-Design Is Not:
- Having a meeting upfront, and then parallel working groups that then mash separate results together into a compromise implementation
- Having monthly meetings—and then mostly ignoring any changed direction (except for complaints)
『「Co-Design」ってそもそもなんなの?』というようなとぼけた疑問を今更言い出したり、議論しているようでは話にならないのは自明。9ページには"Co-Design Should"の説明がある。究極的には、十分資金的なバックアップのあるベンチャー企業のような組織を立ち上げて、一人のリーダーが責任を負い、複数のグループをまとめて全ての最終決断をする、みたいな構造にしないとまともな計算機を作ることはできない。これは、スーパーコンピューターの歴史を振り返ると結構明白である(例えばBrooks & Blaauwの"Computer Architecture: Concepts and Evolution" ( http://dl.acm.org/citation.cfm?id=548907 )を参照。またトレイシー・キダーの「超マシン誕生」を読む。いますぐ)。それが、日本で公的な資金のものとで実現できるのかというのは、大きな問題ではある。
Shalfのスライドは実際の"Co-Design"について、かなり詳細な議論をしている。ShalfはLBNLで推進されているGreen Flashという気象の問題のための計算機開発のリーダーであり、その言葉には経験に裏打ちされた重みがある。x86命令のなかで全く使われていない命令のテーブルとか、それだけでも面白い。以前Green Flashについて見たスライドでは、とにかくTensillicaのシステムでどうにかする、という印象しかなかったが、このスライドは変化が見られる。ポイントは、計算機のためのCHIPを作るの時に、一番コストがかかるのはアーキテクチャや設計自体ではなく、その色々なレベルでの検証であるということ。その解決策のひとつは、すでに検証済みのIPを組み合わせるということで、この場合でも組み合わせたシステムの検証は必要だから、そこはFPGAでエミュレーションして、設計と検証のサイクルをできるだけ短い時間で行うという方法論が示されている。そのほか、COTSは今は"commodity”ではなくて、現在は検証済みIPが"commodity"なんだというのは鋭い(42ページ)。COTSではpetascaleでもまともなシステムを構築はできないのというのは全く正しくて、それをできると言い張るのは幻想と妄想の組み合わせにすぎない。
Shalfのインタビュー記事も興味深い。http://insidehpc.com/2010/08/12/rock-stars-of-hpc-john-shalf/
自身が計算機工学や計算機科学の勉強や研究をしてきて、その途中で天体物理学や相対論のための並列シミュレーションフレームワークの開発に関わってきた経緯を話した上で、
I remember the perspective I had when I was in each of those different roles (when in EE, I thought the scientists were all just bad programmers, and when working for the apps group, I thought the hardware architects were just idiots who would not listen to the needs of the application developers)
異なる立場というのは「計算機」側と「アプリ」側。
エントリのタイトルの意味は、この分野で研究者をやるのなら、コンピューターのことは所詮1年も勉強すれば超最先端までいけるのだから後回しにして、まずはもっと時間がかかる科学や工学の考え方や現在の問題点を理解することを最初にやりましょう、という大学院教育への個人的な意見。Co-Designと無関係ですか?
最近のP3M
Holmらによる一連の論文をリストする。完璧ではないかもしれない。最初の論文をもとに、宇宙論的シミュレーションのため、短距離成分の密度分布としてS2 shapeを採用したP3Mの定式化についてはこちら(このpdfは個人的なメモであり随時アップデートされる。無保証)。
How to mesh up Ewald sums. I. A theoretical and numerical comparison of various particle mesh routines
Deserno and Holm 1998
http://dx.doi.org/10.1063/1.477414
Ewald和のP3M法による定式化をあらためてやり直し、P3Mやその類の方法(PME, SPME)の中では、P3Mが最もよいということを示した。根本的には、新しいことをやっているわけではないが、Hockney&Eastwood(1988)と比べると、非常にわかりやすい。
How to mesh up Ewald sums. II. An accurate error estimate for the particle–particle–particle-mesh algorithm
Deserno and Holm 1998
http://dx.doi.org/10.1063/1.477415
上の論文の続きで、そこでのP3Mの誤差評価の式は、Green関数と、meshの数、boxの大きさなどを決めると、mesh点での総和として数値的に評価できるが、その演算量は無視できるほど小さくはない。そこで、P3Mの誤差評価の式を近似的に計算する方法を提案。近似手法でも十分正確な誤差評価ができるので、必要な精度が与えられた時に、P3Mの最適なパラメーター(mesh数や短距離力の範囲)を楽に決める方法論を示した。
The optimal P3M algorithm for computing electrostatic energies in periodic systems
Ballenegger, Cerdà, Lenz and Holm, 2008
http://dx.doi.org/10.1063/1.2816570 airxiv:0708028
P3Mでの最適化されたグリーン関数は、加速度の誤差を最小化するように選ばれているが、この論文では、分子動力学などで必要なエネルギーを計算するための、エネルギーの誤差を最小化するようなグリーン関数の定式化している。実際上は、結果はそれほど大きく違うわけではないようではある。
How to convert SPME to P3M: influence functions and error estimates
Vincent Ballenegger, Juan Jose Cerdà, and Christian Holm, 2012
http://dx.doi.org/10.1021/ct2001792
SPME(Smoothed Particle Mesh Ewald)をP3Mのフレームワークで捉え直す。まだ読みかけ。
並列化されたTreeコードのサーベイ
総論
重力多体問題のために実装されて発表された、並列ツリーコードについてまとめる。できるだけそれまでになかった新しいアイデアが導入された論文を古い順にとりあげているので、この分野の全てのコード・実装を取り上げているわけではない。並列ツリーコードの特徴は、以下の凡例にある三つのポイントで分類できるので、各項、それを最初に提示した。
凡例
| Basic Data structure (BD) | 主要なデータ構造 |
| Domain Decomposition (DD) | 領域分割の手法 |
| Parallelization (P) | 並列化の方針 |
Parallel Hierarchical N-body Methods (Salmon 1990, PhD thesis)
論文がどこにあるのか検索中。「Parallel Computing Works!」に書いてあったかもしれない。
Parallel Hashed Oct-Tree (Warren & Salmon 1993)
| BD | Morton key and Hash based Oct-tree |
| DD | Morton or Peano-Hilbert ordering |
| P | Locally Essential Tree(LET) |
ツリーのデータ構造として、Barnes&Hut(1986)のFortranでの実装では、八分木をポインタ(のようなもの)で表現していた。この素直な実装は、ある節(以下cell/セル)の粒子が少ない場合には、効率が悪い。そこで、fully threaded treeという方法では、八分木の代わりに2つのポインタでツリーを表現できる。というのは、この論文とは関係ない背景知識で、この論文ではhashを使って直接ツリー構造を保持するという手法を提案している。ハッシュに使うキーはMortonキーと呼ばれる、三次元の粒子座標を一次元の値にマップしたものである。Mortonキーは、3 bitごとに区切られていて、八分木のある階層のどの三次元象限にいるかに対応しており、このキーが計算できると、簡単にツリー上の上の階層や下の階層のキーを計算できる。粒子の分布を一次元であらわすことができるのなら、これほどよいことはないが、問題はこの一次元のキーが疎であること。そこでWarren&Salmonは、配列をhashで置き換えてこの問題を解決した。このhashはMortonキーを入力として、粒子のindexを返すようなものである。これにより、あるセルの子セルを全て数え上げる、などの典型的なツリーの処理は、子セルのキーを計算して(自分のキーに3bitをつけたす)、hashから子セルのindexを得ることで実現できる。さらに、並列化でもMortonキーの性質を利用すると、全プロセッサがひとつのglobalな木を構築すると仮定した場合、個々のプロセッサは自分の粒子のMortonキーを計算してローカル木を作るだけでよい。Mortonキーは全プロセッサで一元化されているので、あるセルのデータがどのプロセッサにあるのかは、簡単に求めることができる。これを利用して、彼らはLocally Essential Tree(LET)という方法を提案した。これは、あるローカル木の粒子と相互作用する他プロセッサの粒子とセルだけを含むような木である。LETが構築できれば、その後のツリーに関わる演算は通信なしでできる。Mortonキーを使えば、LETを得ることは原理的には難しくない(実際はきっと面倒)。Mortonキーのよい性質は、2つの粒子のキーの値が近い場合には、粒子同士が空間的に近いところにマッピングされることである(このようなキーに基づいて粒子の座標をつないで得られる曲線は、その意味で空間充填曲線とよばれる。空間充填曲線の考え方は、メモリアクセスの局所性を高めるのに有用なので、HPCではよく使われるアイデアのひとつ)。ただし、Mortonキーでソートした場合、一部空間でのジャンプが含まれるため、より空間的な局所性の高いマッピングがPeano-Hilbert(PH)キーとよばれる。これも空間充填曲線の一つである。Warren&Salmonは、粒子の領域分割にはPHキーを使っている。
Parallel Tree Code (Dubinski 1996)
| BD | Oct-Tree with Linked List |
| DD | Orthogonal Recursive Bisection(ORB) |
| P | LET |
J.SalmonのPh.D Thesis(1990)で提案されている、ORBによる領域分割を利用した実装。ORBでは、粒子を含んだ領域を再帰的に二分割する。単なる八分木のように等体積になるように分割するのではなく、ニ分割する際には両側で必要な計算量が等しくなるように分割する。分割する面の向きは、原理的には任意の方向にできるが、このコードではxyz軸に垂直な面でcyclicに分割をする。ORBで分割された各プロセッサの粒子は、個々にローカルな木を構築しする。そのあとLETを作成するという部分は、Warren&Salmonと同じである。"with Linked List"と書いた意味は、上記"fully threaded tree"のこと。
Forest Method (Yahagi, Mori & Yoshii 1999)
| BD | Oct-Tree |
| DD | Forest Method |
| P | LET |
この論文のポイントは、"Forest Method"と名付けられた、新たな領域分割法を提案していることである。これはボロノイ分割による領域分割と、そのボロノイ領域を活用したロードバランシングがみそである。ボロノイ領域により粒子を分割すると、個々のプロセッサの担当する粒子分布は球状に近くなる。一方で、ORBのような分割方法では、粒子分布はどうしても直方体になってしまう。三次元の立体で表面積と体積の比が一番小さいのは球であり、領域分割された並列計算においては、この比によって通信量が決定されるため、可能であれば領域分割は球に近いほうが有利である。また、ボロノイ分割では、他の領域との境界は、それぞれの領域の中心点を結んだ直線を垂直に分割する面である。本来のボロノイ分割では、分割面はこの直線の中点を通るようなものである。Forest Methodでは、この分割面をロードバランスに応じて、中点からずらすことで、各プロセッサの領域の体積を調整し、それによってロードバランスを実現する。この時に「計算負荷(ロード)」の平均化に、拡散方程式を利用していることも特徴である。領域分割が面でおこなわれているので、LETを構築することは、比較的簡単になる。
Gadget-1 (Springel, Yoshida & White 2001)
| BD | classical Oct-tree |
| DD | Morton ordering? |
| P | Ring Method |
天体物理学シミュレーション業界では最も広く使われている実装の初期のもの。ポイントは、ローカルツリーを作った後で、LETを作ることをしないで、力を計算する粒子(GRAPEの用語でいうとi粒子)の情報を通信する。この時に各プロセッサが、リング上に接続されていることを仮定して、バケツリレー式にi粒子のデータを隣に渡す。受け取ったi粒子に対して、ローカルツリーからの加速度(重力とSPH)を計算し、次はi粒子のデータとともにこの加速度も通信する。このような手法を採用している理由は、Gadgetではではblocked individual timestep schemeを使っていて、つまりある時間に積分する粒子は何らかの条件で選んだ粒子のみである。この選ばれた粒子の数は、通常全粒子数よりかなり少ないので、LETを作るコストが馬鹿にならない。欠点は、この方法ではプロセッサが多くなると性能が落ちることである。大きな利点は、プログラムが非常に単純になること。Gadgetでは、ツリー構築の時間を最小限にするため、粒子が動いた場合にも、全体の木構造を作り直すのではなく、局所的な変更のみを反映させるなど、詳細な最適化をおこなっている。これは実際には結構大変なので(セルの重心や四重極モーメントの予測子を計算する!)、LETを作ったほうが実は簡単かもしれない。宇宙論的シミュレーションで必要な周期境界条件は、Ewald和によって得られた加速度場を利用している。
Gasoline (Wadsley, Stadel, Quinn 2004)
| BD | Binary-Tree |
| DD | ORB |
| P | dynamic |
GasolineはPKDGRAV(Stadel 2002 Phd http://adsabs.harvard.edu/abs/2001PhDT........21S )を拡張し、元々は重力のみだったものに、SPHを加えたコードである。このコードが、他の実装と最も違うところは、基本的なデータ構造として二分木を採用していることである。ツリーが出来てしまえば、二分木か八分木に本質的な違いはないが、ツリー構築の方法がbottom upかtop downかという違いがある。一方で、今では一番下の階層にある節の粒子数が1個になるような純粋な八分木を構築することは無駄であるとわかっているので、Gasolineでも一番下の階層の粒子数は8個以下とかになっている。その意味では、Gasolineで採用しているものは、PKDGRAVの論文のタイトル通り"k-d"ツリーである(ほぼ二分木。他のコードはほぼ八分木)。領域分割はORBである。並列化の方法は、ORBツリーにたいして直接ツリーウォークを行う方法である。つまり、各プロセッサはORBツリー(その下の階層は各プロセッサのローカルツリー)のツリーの根から直接ツリーをたどっていき、ローカルではないセルにたどり着いたら、暗黙的に(?)通信をおこなうという方法である。周期境界条件の扱いはGadget-1と同じ。Gasolineのその他の部分には目新しい部分はないので省略。
PKDGRAVについてはwebページがあったので、詳しくはこちら:http://hpcc.astro.washington.edu/faculty/trq/brandon/pkdgrav.html
Fast Parallel Treecode with GRAPE (Makino 2004)
| BD | classical Oct-Tree |
| DD | extended ORB |
| P | opitimized LET |
ORB分割では、並列プロセッサの数が2のべき乗であることを仮定していて、ある軸の方向には必ず二分割しかしないため、任意のプロセッサ数では利用できない。この実装では、その制限を排除し、分割数を任意として、より幅広い並列プロセッサでORB likeな手法を使う。もう一つORBと異なるのは、LETの構築の仕方である。ORBでは、各プロセッサの持つローカルな粒子群が、ORBによって作られたツリーとなっているので、他のプロセッサからは必要最低限に枝切りしたツリー(LET)をもらえばよい。結果、グローバルなツリーは、ORBツリーとローカルな八分木ツリーの組み合わせとなる。この実装では、ローカルなツリーを作るとのは同じで、そのプロセッサに属する粒子と相互作用する粒子とセルのリストを作り、それをローカルなツリーに追加するというアイデアを採用している。これにより、個々のプロセッサの持つツリーはほぼ最適となる(ORB+ローカルツリーでは、幾何学的に近い粒子が別のノードに割り当てられてしまう)。
Gadget-2 (Springel 2005)
| BD | Oct-Tree + Mesh |
| DD | Peano-Hilbert ordering |
| P | TreePM |
Gadget-2は、Gadget-1の後継であるが、実装の詳細は大きく変わっている。この業界のスタンダードなコード。TreePM法とは、重力のような長距離力を、短距離成分と長距離成分に分離して、それぞれを別の重力ソルバーで解く手法であり、名前が表すとおり、短距離にはツリーを、長距離にはPM法特にFFTベースでPoisson方程式を解く。この方法は本質的にはParticle-Particle Particle-Mesh(PPPM)の拡張であり、短距離成分の計算をツリーで加速するということがポイントになる。なおTreePM法自体はSpringelの提案ではなく、Xu 1995によって提案された。Gadget-2ではより精密化された定式化によるSPHを採用しているだけでなく、SPHと組み合わせた多相星間物質のモデルや、星形成モデル、冷却関数等々、様々な物理過程も含んでいる。N体シミュレーションで最も大規模な計算のひとつはGadget-2(の特殊な最適化バージョン)でおこなわれた。TreePM法なので、周期境界条件はPMの部分をFFTで解くことで、自然と満たされている。
PPPM and TreePM Methods on GRAPE Systems (Yoshikawa&Fukushige 2005)
| BD | Oct-Tree + Mesh |
| DD | slab |
| P | TreePM |
GRAPE用に最適化されたTreePMコード。TreePMでは、短距離成分の計算はカットオフをもったようなカーネルによる和に帰着するので、ほとんどSPHの計算と変わらない。そのため、そもそもグローバルなツリーを作る必要はない。この実装では、領域分割としては1次元のslab分割を採用している。slab分割は一般的には、あまりスケーラブルではないが、この実装でslab分割を採用している理由は、個々のノードがGRAPE-6Aをもつクラスターをターゲットとしているからである。GRAPE-6Aをもつクラスターでは、ノードあたりの重力演算能力が普通のx86_64コア1つより10倍以上高速である。これは何を意味するかというと、同じ計算をするのにノード数を十分の一以下にできるということである。MPPで1024コア必要な計算を、GRAPEのクラスターであれば32ノードとかで実現できる。その意味では、GRAPEやGPUのような加速演算装置を持ったクラスターは、必要なMPIプロセスの数を減らすことができるので、並列ツリー法には適したアーキテクチャといえる。この論文は、ノード数が数十であれば、PMのメッシュ数が512以上もあれば、slab分割であっても十分活用できることを示している。
GreeM (Ishiyama, Fukushige & Makino 2009)
| BD | Oct-Tree + Mesh |
| DD | extended ORB |
| P | TreePM |
Yoshikawa&Fukushige(2005, YF)のTreePMコードに、Makino(2004, M)提案のツリー法を組み合わせたもの。M2004, YF2005ともに、GRAPEと組み合わせたツリーコードであるが、GreeMはGRAPEボードをターゲットとはしていない。国立天文台のCRAY XT-4をターゲットとして開発された(のだろう)。そのため、ノードあたりの演算性能が落ちるため、YF2005とは異なり、領域分割はORBベースのものに変更されている。ただし、GRAPEの代わりに、Nitadori(2006)による、SSE2を利用した高速なGRAPE互換x86_64プロセッサ用ライブラリPhantomを利用している。Phantomを使うことで、1コアあたりの重力演算性能として10 - 30 Gflopsを得ることができる。CRAY XT-4では、NP = 1024コアまでよくスケーリングしていて、これはGadget-2よりもよい。
OpenCLで実装されたSPHのパフォーマンス比較
OpenCLでSPH法のプログラムを実装し、様々なプロセッサで性能を比較している。
このSPHのプログラムは、http://arxiv.org/abs/1112.4539 の論文で発表したGPUでの直接treewalkを拡張したもので、この論文のAppendixにある、OpenCL Cで書かれたコードがベースとなっている。我々の手法は、treewalkだけをGPUなりmulti core CPUで実行するというものであり、我々の意見ではこうするのが一番性能がでる。この論文は重力相互作用場合の性能評価をしているが、この方法の拡張で、SPHの近接相互作用の和を直接計算することができる。粒子をキャッシュにやさしい順番に並び替えるということも同じく効果的である。 さらに、現時点のコードでは、ホスト計算機でのtreeのconstructionを含めて、全体的に実装しなおして高速化した。これは、GPUによりtreewalkが高速になった反面、今度はtree constructionがボトルネックになってきたからである。上記論文のデータでは、80万粒子の場合、tree constructionには約30%の時間がかかっている。アムダールの法則を持ち出すまでもなく、より大きい粒子の計算では、GPUの高速さ(ベクトル計算機として)の意義が失われてしまう。この論文のコードでは、tree constructionには、シングルスレッドで八分木のポインタに基づいた方法を使っていた。これはBarnesのオリジナルのFortranでの実装とほぼ同様である。今のコードではMorton keyを並列ソートしてから、直接Next/Moreのポインタを生成する手法とした(Next,Moreの意味は論文参照)。
このNext/Moreを使う方法は、文献によると"Brother/child representation"と呼ばれるらしい(参照: http://onlinelibrary.wiley.com/doi/10.1111/j.1467-8659.2007.01104.x/abstract )。あるいは、CS業界ではfully threaded treeと呼ばれるらしい。treewalkは再帰関数として記述することができ、非常に美しいアルゴリズムの一つであるが、再帰関数はそのまま扱うとスタックの操作が頻繁になるため、ループに比べると性能がよくないかもしれない。末尾再帰はループに変換することができる。つまりNext/Moreのポインタを使うことで、treewalkを再帰を使わずに、また明示的なスタック処理も必要なく扱うことができる。これはGPUに向いたアルゴリズムで(最初に提案されたのはDubinskiの修士論文(1988) or Makino&Hut 1989 ?かもしれない)、Makino(1990)にて提案されたtree法のベクトル化手法の一つである。実はこの時、他に二人の著者(BarnesとHernquist)がそれぞれ別のベクトル化を提案して、この三つの論文はまとめてJournal of Computational Physicsに掲載されている。このMakinoによる末尾再帰のループへの変換の応用といい、そもそもBarnesによる八分木ツリーの提案も、彼らがIASに滞在していた頃におこなわれている(ような気がする)。しかも、これはどちらもConnection Machineに関係していて、そしてそれはMITのLISP/Schemeハッカー達の多大なる影響のもとで発明されたと勝手に思っているが、どうだろうか?機会があれば、本人に尋ねてみよう。リンク。と、ものすごい脱線はさておき。
この方法の利点は、treeのデータ構造として必ずしも八分木を想定しなくてもよいことである。そもそもオリジナルのtree法では、treeの各ノードの粒子数が1個になるまで、再帰的にtreeデータを構築していた。だが、粒子数が増えてきた時には、1個になるまでノードを追加していくのは時間がかかるし、実際問題必要のないことが90年(?)頃に発見されて、特にGRAPEとtree法を組み合わせる場合、通常はノード内の粒子が数十個を下回ったらもうノードを作らないほうが速いし、力の精度もよい。こうすることで、単純には元々のtree法の再帰的動的であるという美しさが失われてしまうが、実際上速いのに越したことはない。我々の方法ではソートされた粒子のリストから、基本的には八分木のデータを生成する。ただし八分木のポインタは使わない。また、下の階層のノードでは、ノード内の粒子数が指定した値を下回った場合には、それ以上の階層を作るのをやめて、代わりにNextポインタで粒子を直接リンクする。既にソートされているものをポインタを使ってリンクしなおすことで、実は効率が落ちてしまうが、こうするとtreewalkカーネルは修正をする必要がない。これは、実効的には、最下層ノードはN分木になっていて、その上は八分木になっているようなツリーになる。またポインタを使うことで、上の階層の八分木も保持する必然はなくなる。幾何学的に局所性が保たれるのであればN分木に変更してもよいということになる。これが意味を持つのは並列化をする時である。
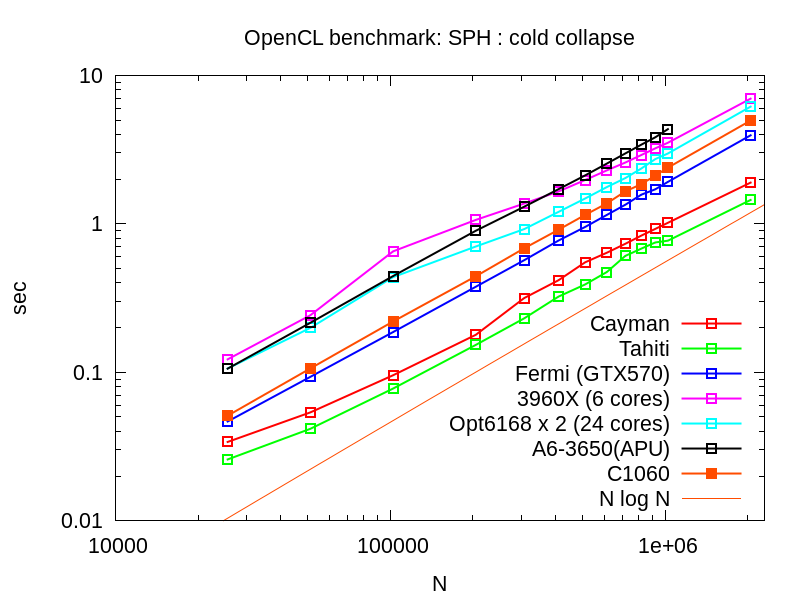
さて、性能評価は以下の図。図は随時アップデートされるかもしれない。やっている計算は、いわゆる冷たいガス球の収縮で、hydrodyamicsとself gravityを解いている。状態方程式は理想気体で、もちろん断熱である。粒子数を横軸として1 stepあたりの平均計算時間をプロットした。計算時間はメインループの計算時間より算出しているので、当然tree constructionやGPUとのデータ転送等すべてを含む。演算は全て単精度。IntelのCPUではIntelのSDKを、AMDのGPUとCPUはAMDのSDKを、NVIDIAのGPUではNVIDIAのSDKを使っている。
以下コメント:
- OpenCLのSDKは使いものになる。この結果は、コードベースはひとつで各社のSDKで問題なく動作した。
- GPUではTahitiが一番速い。
- FermiのほうがGT200より速い。
- 24 core機がCPUの中では一番速い。
- Sandybridge-Eは24 coreのOpteronとあまり性能が変わらない。
- APUの結果はGPUを使った場合。Nの小さい所で大健闘している。次世代のAPUは面白いかも。
。。。
コメントはこちら https://plus.google.com/117333869988556483969/posts/Y144K5p53LM

 rss
rss