トップ：http://galaxy.u-aizu.ac.jp/note/wiki/CAEX2017

課題4：乗算の実装

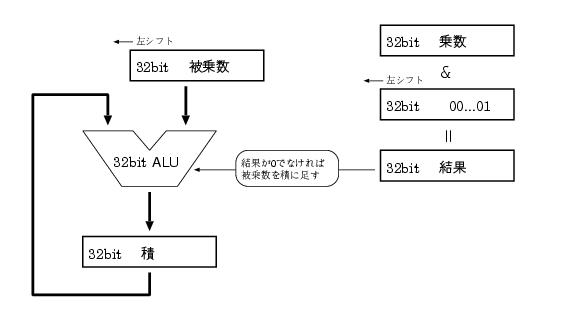
第5版教科書上巻p.177の「3.3 乗算」をよく読んで、乗算をおこなうプログラムを作ってください。 乗数A、被乗数B、積Cは32ビットです。求める乗算結果は64ビットではなく、下位の32ビットだけで十分です。 つまり、乗数と被乗数は最大16ビットまでを仮定してください。 今後演習で設計するMIPSプロセッサは、シフト命令をサポートしていませんので、以下のような工夫が必要になります。

左シフト

1ビット左シフトは2倍することと同等なので加算命令によって実現できます。

シフト命令を使う場合：

sll $8,$9,1

加算命令の場合：

add $8,$9,$9

ここで気をつけなければならないのは、加算によるオーバーフローです。 最上位ビットが1である数を2倍すると（正確には同じ数を足し合わせると）、 最上位ビットで桁上がりを生じるため、add 命令ではオーバーフロー例外が発生します。 xspimでは、このためプログラムが停止するので、 左シフトするための加算はaddではなく、 オーバーフローを無視するadduを使用してください。

一方、演習の後半で設計するプロセッサはオーバーフローをチェックしませんので、 回路シミュレーション時はadduをaddに戻す必要があります。 詳しいことは、該当回の際に説明します。なお、今回作成するプログラムはadduを利用したものを保存しておくこと。

右シフト

1ビット右シフトを他の命令で単純に実現することは困難です。 そこで今回は乗算アルゴリズムとハードウエアの直列バージョン(教科書上巻p.212)に あるアルゴリズムを、左シフトのみを使うように修正して乗算を実現します。

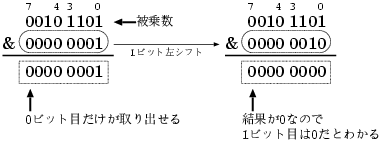
乗算で使われる右シフトは、ビットを下位から順に調べることだけが目的なので、 左シフトを使って同等の機能を実現することができます。

下のように、右シフトの結果と定数1とのandをとる代わりに、 初期値として1をレジスタに入れておき、これを左シフトしたものとand をとるようにします。

シフト命令を使う場合：

  srl $8,$8,1
  andi $9,$8,1

加算命令の場合：

  addi $10,$0,1     # $10に1を代入（前処理）
    :
  addu $10,$10,$10  # 左シフト。通常でslr命令だった部分に相当
  and $9,$8,$10     # 通常でandi命令だった部分に相当

この様にして各ビットが1か0かを調べられます。

シフト命令を使う方法（上）だと結果は 0…01（32ビット） か 00…0（32ビット）の2通りだけですが、 加算命令を使用した方法（下）だと、そのビットが0のときは 00…0 ですが、そのビットが1だった場合、 その結果もそれが何桁目かによって、結果を左にシフトしています。 ですから、結果が0であるか否かで条件分岐をすることになります。

初期化部分

        .data 
A:      .word 13 
B:      .word 37 
C:      .word 0

       ... 必要な変数の領域を追加する ....
        .text 
main:       ... プログラムを書く .... 


exit:   j exit

作成ファイル名は「ex02_p4.s」としてください。

課題5：行列積

以下のC言語で書かれた行列乗算のプログラムを参考にして、行列積C = A x Bを計算するプログラムを作ってください。

行列A

0  1  0  0
2  0  0  0 
0  0  0  3
0  0  4  0

行列B

1  2  3  4
5  6  7  8 
9 10 11 12
13 14 15 16

テンプレート

作成ファイル名は「ex02_p5.s」としてください。

        .data 
A:      .word 0 
        .word 1 
        .word 0 
        .word 0 
    ... 配列Aの要素を書く .... 

B:      .word 1 
        .word 2 
        .word 3 
        .word 4 
    ... 配列Bの要素を書く .... 

C:      .space 64 ## 結果行列の保存用

       ... 必要な変数の領域を追加する ....
        .text 
main: 
exit:   j exit

C言語バージョン

#include <stdio.h>
main()
{
  static int mat1[4][4] = {
    { 1, 0, 0, 0 },
    { 0, 1, 0, 0 },
    { 0, 0, 1, 0 },
    { 0, 0, 0, 1 },
  };
  static int mat2[4][4] = {
    {  1,  2,  3,  4 },
    {  5,  6,  7,  8 },
    {  9, 10, 11, 12 },
    { 13, 14, 15, 16 },
  };
  static int result[4][4];

  int  i, j, k;
  int  s;
  int  m1, m2;

  /* 行列の乗算 */
  for( i = 0; i < 4; i++ ) {
    for( j = 0; j < 4; j++ ) {
      s = 0;
      for( k = 0; k < 4; k++ ) {
	mask = 1;
	m1 = mat1[i][k];  /* 被乗数 */
	m2 = mat2[k][j];  /* 乗数 */
        s += m1 * m2
      }
      result[i][j] = s;
    }
  }

  /* 結果の表示 */
  for( i = 0; i < 4; i++ ) {
    for( j = 0; j < 4; j++ ) {
      printf("%3d", result[i][j]); 
    }
    printf("\n");
  }
}