Reservoir Computing とは

Recurrent Neural Network(RNN)の一種。シンプルなNeural Network(NN)は、入力だけで出力が決まる非線形関数であるが、 RNNは入力とNN内部の状態の組み合わせで出力が決まる非線形関数。 RNNは順次入力された一連のデータから、なんらかの情報を保持している。Long short-term memory(LSTM)が最近はよく使われている。

他のRNNと比べたReservoir Computing(RC)の特徴は、ちょっと変わったニューラルネットワーク https://qiita.com/kazoo04/items/71b659ced9dc0342a2b0 に解説がある。隠れ層の部分にたくさんのニューロンがあって、隠れ層内部の接続と入力や出力層との接続はランダムに決めるというところがポイントらしい。

実際の脳内のニューロンは、物理的にも不可能なので、全対全で接続されているわけはなく、基本的は近くのニューロン同士が接続され、時々遠くニューロンとの接続があるという、簡単ではないネットワークトポロジとなっている(要出典)。RNNではない普通のNNの学習では、学習中にランダムにニューロン同士の接続を切るdropoutという手法が有効な場合があり、これはRCの性質とよく似ているのではないだろうか。

RCが総称で、細かい違いによりLiquid State Machine(LSM)、Echo State Network(ESN)などがあるが、本質的にはどれも同じ。

RCをアナログ的に実現する方法についてもいろいろと提案されている。https://arxiv.org/abs/1709.10211 など。後で追記。

論文のメモ

A Practical Guide to Applying Echo State Networks

https://link.springer.com/chapter/10.1007%2F978-3-642-35289-8_36

RCのreview。タイトルで検索するとPDFも落ちている。

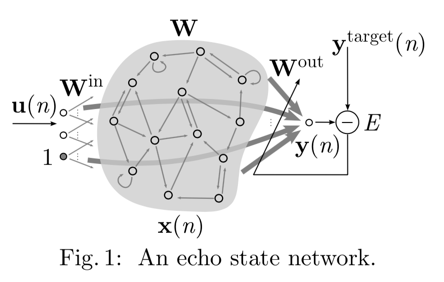
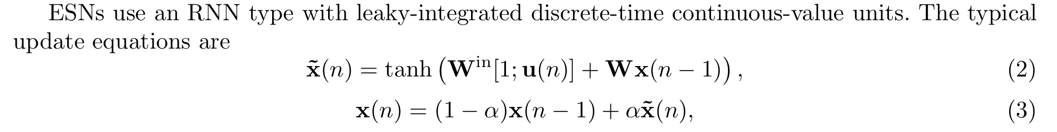
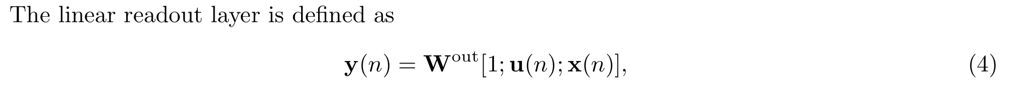
x(n)は隠れ層のニューロンの出力を表す。それらを接続しているのがWという行列。activation functionはtanhでなくても、他のものでもいい。WやWin,Woutは、最初にランダムに設定して、WとWinは学習中には更新しない。教師データとの誤差からWoutを誤差逆伝搬でアップデートする(はず)。

Wは、ニューロン間の接続を表す隣接行列になる。初期化する時に、そのそのスペクトル半径を調整することで、RCの性能を調整できるらしい。(よくわかっていない)

Using Machine Learning to Replicate Chaotic Attractors and Calculate Lyapunov Exponents from Data

https://arxiv.org/abs/1710.07313

カオス系の方程式がうまく学習できましたという論文。

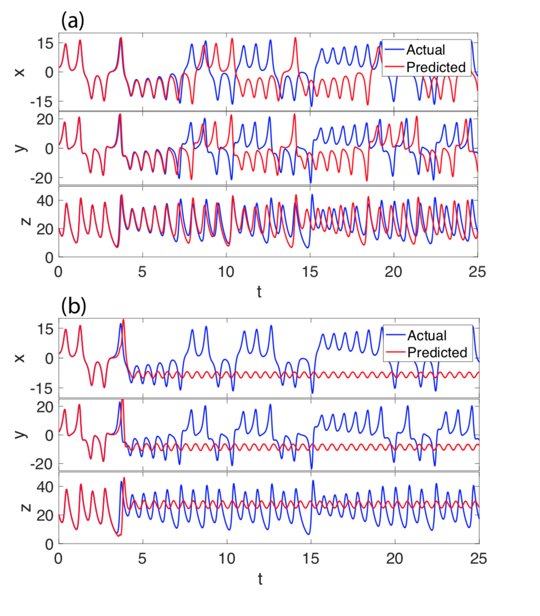
この図はローレンツ方程式。論文のメインはは2次元のカオスな方程式を学習。

Using a reservoir computer to learn chaotic attractors, with applications to chaos synchronisation and cryptography

https://arxiv.org/abs/1802.02844

この論文もカオスの性質がある方程式を学習してみたもの。複数のカオス系を相互作用をさせると、それらが同期するという性質も、RCにより学習ができた。これを応用することで、カオス暗号をcrackできる可能性がある。

参考動画 メトロノーム同期(100個) https://www.youtube.com/watch?v=suxu1bmPm2g

FPGA-Based Stochastic Echo State Networks for Time-Series Forecasting

https://www.hindawi.com/journals/cin/2016/3917892/

単純に考えるとRCの実証論文というのは、上のx(n)の式などを浮動小数点演算演算を使って実装しているものであるが、それを整数演算のみで考えて、FPGAに実装して評価したという論文。

Integer Echo State Networks: Hyperdimensional Reservoir Computing

https://arxiv.org/abs/1706.00280

これも、量子化して整数演算のみで実装する。入力データは、数値でも文字列でもなんでもいいが、何らかの符号化で整数値にマップする。このような符号化のひとつがhyperdimentional computing(HDC)とよばれるもので、この論文ではその符号化を使って、入力の数値(浮動小数点数)を整数に変換して、整数でESNを実装している。ネットワークの構造は全く同じで、浮動小数点で直接実装した場合との比較。

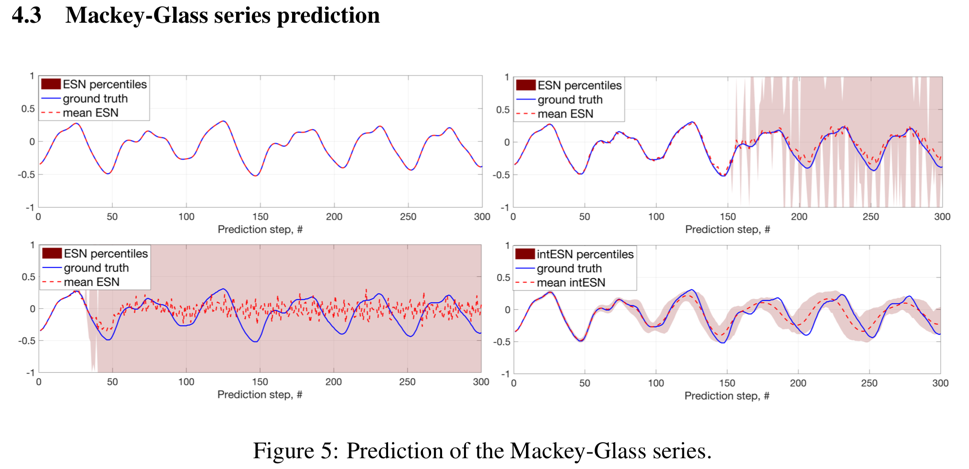
Reservoir computing & extreme learning machines using pairs of cellular automata rules

https://ieeexplore.ieee.org/abstract/document/7966151/

符号化量子化で整数演算に帰着するなら、セルオートマトンでも等価に実現できる、という論文。1次元のセルオートマトンのうち、3入力1出力(3点ステンシルと同じ)の場合について、どのオートマトンが、よい性質をもつかを検証している。この場合オートマトンのパターンは全部で128ある。実際上の方法として、2つの別のオートマトンを組み合わせる。全部で128 x 128の組み合わせがあり得る。

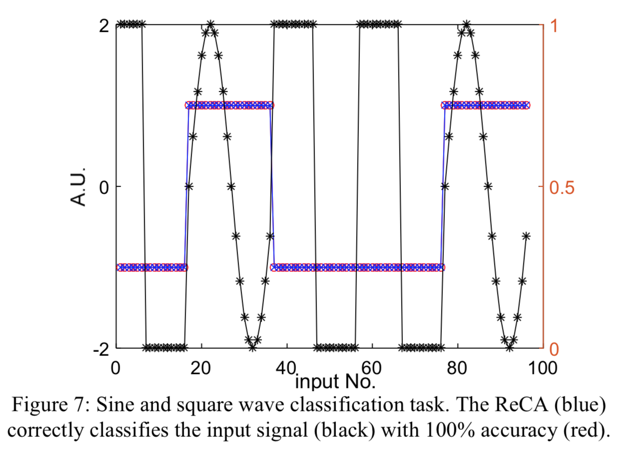
この方法で矩形波と三角関数の識別が100%の精度でできているなど。