#概要 重力多体問題のために実装されて発表された、並列ツリーコードについてまとめる。 できるだけそれまでになかった新しいアイデアが導入された論文を古い順にとりあげているので、 この分野の全てのコード・実装を取り上げているわけではない。 並列ツリーコードの特徴は、以下の凡例にある三つのポイントで分類できるので、 各項、それを最初に提示した。
###凡例
| アルゴリズム | |
|---|---|
| Basic Data structure (BD) | 主要なデータ構造 |
| Domain Decomposition (DD) | 領域分割の手法 |
| Parallelization (P) | 並列化の方針 |
Parallel Hierarchical N-body Methods (Salmon 1990, PhD thesis)
論文がどこにあるのか検索中。「Parallel Computing Works!」に書いてあったかもしれない。
Parallel Hashed Oct-Tree (Warren & Salmon 1993)
| BD | Morton key and Hash based Oct-tree |
| DD | Morton or Peano-Hilbert ordering |
| P | Locally Essential Tree(LET) |
ツリーのデータ構造として、Barnes&Hut(1986)のFortranでの実装では、 八分木をポインタ(のようなもの)で表現していた。この素直な実装は、 ある節(以下cell/セル)の粒子が少ない場合には、効率が悪い。 そこで、fully threaded treeという方法では、八分木の代わりに2つのポインタでツリーを表現できる。 というのは、この論文とは関係ない背景知識で、 この論文ではhashを使って直接ツリー構造を保持するという手法を提案している。ハッシュに使うキーはMortonキーと呼ばれる、三次元の粒子座標を一次元の値にマップしたものである。Mortonキーは、3 bitごとに区切られていて、八分木のある階層のどの三次元象限にいるかに対応しており、このキーが計算できると、簡単にツリー上の上の階層や下の階層のキーを計算できる。粒子の分布を一次元であらわすことができるのなら、これほどよいことはないが、問題はこの一次元のキーが疎であること。そこでWarren&Salmonは、配列をhashで置き換えてこの問題を解決した。このhashはMortonキーを入力として、粒子のindexを返すようなものである。これにより、あるセルの子セルを全て数え上げる、などの典型的なツリーの処理は、子セルのキーを計算して(自分のキーに3bitをつけたす)、hashから子セルのindexを得ることで実現できる。さらに、並列化でもMortonキーの性質を利用すると、全プロセッサがひとつのglobalな木を構築すると仮定した場合、個々のプロセッサは自分の粒子のMortonキーを計算してローカル木を作るだけでよい。Mortonキーは全プロセッサで一元化されているので、あるセルのデータがどのプロセッサにあるのかは、簡単に求めることができる。これを利用して、彼らはLocally Essential Tree(LET)という方法を提案した。これは、あるローカル木の粒子と相互作用する他プロセッサの粒子とセルだけを含むような木である。LETが構築できれば、その後のツリーに関わる演算は通信なしでできる。Mortonキーを使えば、LETを得ることは原理的には難しくない(実際はきっと面倒)。Mortonキーのよい性質は、2つの粒子のキーの値が近い場合には、粒子同士が空間的に近いところにマッピングされることである(このようなキーに基づいて粒子の座標をつないで得られる曲線は、その意味で空間充填曲線とよばれる。空間充填曲線の考え方は、メモリアクセスの局所性を高めるのに有用なので、HPCではよく使われるアイデアのひとつ)。ただし、Mortonキーでソートした場合、一部空間でのジャンプが含まれるため、より空間的な局所性の高いマッピングがPeano-Hilbert(PH)キーとよばれる。これも空間充填曲線の一つである。Warren&Salmonは、粒子の領域分割にはPHキーを使っている。
Implications of Tree methods for multiprocessor architectures (Singh, Hennessy & Guputa 1995)
http://dl.acm.org/citation.cfm?doid=201045.201050
この論文だけは、他のエントリと異なり、 コンピュータアーキテクチャの研究者(へね)がツリー法をマルチプロセッサで性能評価した論文である。 第一著者であるSinghの博士論文 “Parallel hierarchical N-body methods and their implications for multiprocessors” (Doctoral Dissertation, Stanford Univesity, 1993)を投稿したものと思われる。
すごく長い。以下、Section 9のメモを。
ここでは、SalmonのLETを使ったツリー法について色々と議論している。 論調は、LETとメッセージパッシングは使えねー、ってこと。 ただし、これは90年代前半の仕事なので、今とは対象としている問題のサイズが圧倒的に小さい。 この部分である意味かなりdisられている、Salmonの結果でも512プロセッサで10万粒子とからしい。
ちょっとおもしろかったので引用。
The difference is also demonstrated by our experience with having groups of graduate students implement the application on SAS-CC and message-passing machines, in a ten-week parallel programming project course at Stanford University. The SAS versions were produced very quickly, and yield very good speedups on the DASH multiprocessor. A message-passing version, however, is yet to be completed within the time allotted for the project
この部分の前に、Salmonの提案によるMPを使ったLETのツリー法は、 SASでの実装より数倍時間がかかったと書いてある(誰が?)。 その上で、ツリー法の実装をStanfordの大学院生に10週のプロジェクトとしてやらせてみたら、 共有メモリ(SAS-CC)とMessage-paasing(MP)の生産性の「違い」が示されたという。 SAS-CCとはshared address space-cache coherentの略。著者らはSAS-CCな計算を推しているのは言うまでもない。
まず、LETではメモリ使用量が非常に多くなる。 これはLETでは保守的にTreeを構築するので、 結果的には無駄な粒子とノードをLETに追加してしまうため。 よって、メモリ利用量も多いし、そのためのデータの交換に必要なデータ量も多いし、 それを実現するためのプログラミングも非常に複雑になる。ボロクソである。
一方SAS-CCでのツリーの実装では、データ交換は暗黙的のためプログラミングが簡単であり、 また、本当に必要最低限のデータ交換しか発生しない。 それは、SASでの実装では、LETを構築するのではなく、一つの共有されたtreeを実装するためで、 “Costzone”と呼ばれるロードバランスの手法と対になっている。 利用するメモリ量は、シリアルのコードとほとんど変わらない程度になる(はずである)。 ただし、彼らが議論している粒子数はたかだか16000粒子程度であり(Table 2参照)、 それのための必要なキャッシュ量は16KBとあり、現代には通用しない。 そもそも、現在でも128プロセッサを超えるような共有メモリ機を、 ハード的に実現するのは現実的には非常に難しい(性能が出ない)。
それでも、無理やり彼らの結論を敷衍すると、ハード的に共有メモリを実現することは難しくても、 N-bodyに専用の共有メモリフレームワークを改めて考えて、 まともに実装することには意味があるかもしれない、ということになる。 実際、彼らは仮想ポインタを利用したツリーの実装と、 ハッシュ値を使ったツリーの実装があり得ると提案していて、 これらはある種N-Bodyのための共有メモリフレームワークになっている。 脚注には、ハッシュ値を使ったツリーの実装を「この論文」を書いている時に、 Salmonらがおこなっているとある。これは上のHOT論文のことである。
Parallel Tree Code (Dubinski 1996)
| BD | Oct-Tree with Linked List |
| DD | Orthogonal Recursive Bisection(ORB) |
| P | LET |
J.SalmonのPh.D Thesis(1990)で提案されている、ORBによる領域分割を利用した実装。ORBでは、粒子を含んだ領域を再帰的に二分割する。単なる八分木のように等体積になるように分割するのではなく、ニ分割する際には両側で必要な計算量が等しくなるように分割する。分割する面の向きは、原理的には任意の方向にできるが、このコードではxyz軸に垂直な面でcyclicに分割をする。ORBで分割された各プロセッサの粒子は、個々にローカルな木を構築しする。そのあとLETを作成するという部分は、Warren&Salmonと同じである。“with Linked List"と書いた意味は、上記"fully threaded tree"のこと。
Forest Method (Yahagi, Mori & Yoshii 1999)
| BD | Oct-Tree |
| DD | Forest Method |
| P | LET |
この論文のポイントは、“Forest Method"と名付けられた、新たな領域分割法を提案していることである。これはボロノイ分割による領域分割と、そのボロノイ領域を活用したロードバランシングがみそである。ボロノイ領域により粒子を分割すると、個々のプロセッサの担当する粒子分布は球状に近くなる。一方で、ORBのような分割方法では、粒子分布はどうしても直方体になってしまう。三次元の立体で表面積と体積の比が一番小さいのは球であり、領域分割された並列計算においては、この比によって通信量が決定されるため、可能であれば領域分割は球に近いほうが有利である。また、ボロノイ分割では、他の領域との境界は、それぞれの領域の中心点を結んだ直線を垂直に分割する面である。本来のボロノイ分割では、分割面はこの直線の中点を通るようなものである。Forest Methodでは、この分割面をロードバランスに応じて、中点からずらすことで、各プロセッサの領域の体積を調整し、それによってロードバランスを実現する。この時に「計算負荷(ロード)」の平均化に、拡散方程式を利用していることも特徴である。領域分割が面でおこなわれているので、LETを構築することは、比較的簡単になる。
Gadget-1 (Springel, Yoshida & White 2001)
| BD | Classical Oct-tree |
| DD | Morton ordering? |
| P | Ring Method |
天体物理学シミュレーション業界では最も広く使われている実装の初期のもの。ポイントは、ローカルツリーを作った後で、LETを作ることをしないで、力を計算する粒子(GRAPEの用語でいうとi粒子)の情報を通信する。この時に各プロセッサが、リング上に接続されていることを仮定して、バケツリレー式にi粒子のデータを隣に渡す。受け取ったi粒子に対して、ローカルツリーからの加速度(重力とSPH)を計算し、次はi粒子のデータとともにこの加速度も通信する。このような手法を採用している理由は、Gadgetではではblocked individual timestep schemeを使っていて、つまりある時間に積分する粒子は何らかの条件で選んだ粒子のみである。この選ばれた粒子の数は、通常全粒子数よりかなり少ないので、LETを作るコストが馬鹿にならない。欠点は、この方法ではプロセッサが多くなると性能が落ちることである。大きな利点は、プログラムが非常に単純になること。Gadgetでは、ツリー構築の時間を最小限にするため、粒子が動いた場合にも、全体の木構造を作り直すのではなく、局所的な変更のみを反映させるなど、詳細な最適化をおこなっている。これは実際には結構大変なので(セルの重心や四重極モーメントの予測子を計算する!)、LETを作ったほうが実は簡単かもしれない。宇宙論的シミュレーションで必要な周期境界条件は、Ewald和によって得られた加速度場を利用している。
Gasoline (Wadsley, Stadel, Quinn 2004)
| BD | Binary-Tree |
| DD | ORB |
| P | dynamic |
GasolineはPKDGRAV(Stadel 2002 Phd http://adsabs.harvard.edu/abs/2001PhDT........21S )を拡張し、元々は重力のみだったものに、SPHを加えたコードである。このコードが、他の実装と最も違うところは、基本的なデータ構造として二分木を採用していることである。ツリーが出来てしまえば、二分木か八分木に本質的な違いはないが、ツリー構築の方法がbottom upかtop downかという違いがある。一方で、今では一番下の階層にある節の粒子数が1個になるような純粋な八分木を構築することは無駄であるとわかっているので、Gasolineでも一番下の階層の粒子数は8個以下とかになっている。その意味では、Gasolineで採用しているものは、PKDGRAVの論文のタイトル通り"k-d"ツリーである(ほぼ二分木。他のコードはほぼ八分木)。領域分割はORBである。並列化の方法は、ORBツリーにたいして直接ツリーウォークを行う方法である。つまり、各プロセッサはORBツリー(その下の階層は各プロセッサのローカルツリー)のツリーの根から直接ツリーをたどっていき、ローカルではないセルにたどり着いたら、暗黙的に(?)通信をおこなうという方法である。周期境界条件の扱いはGadget-1と同じ。Gasolineのその他の部分には目新しい部分はないので省略。
PKDGRAVについてはwebページがあったので、 詳しくはこちら:http://hpcc.astro.washington.edu/faculty/trq/brandon/pkdgrav.html
Fast Parallel Treecode with GRAPE (Makino 2004)
| BD | Classical Oct-Tree |
| DD | Extended ORB |
| P | opitimized LET |
ORB分割では、並列プロセッサの数が2のべき乗であることを仮定していて、ある軸の方向には必ず二分割しかしないため、任意のプロセッサ数では利用できない。この実装では、その制限を排除し、分割数を任意として、より幅広い並列プロセッサでORB likeな手法を使う。もう一つORBと異なるのは、LETの構築の仕方である。ORBでは、各プロセッサの持つローカルな粒子群が、ORBによって作られたツリーとなっているので、他のプロセッサからは必要最低限に枝切りしたツリー(LET)をもらえばよい。結果、グローバルなツリーは、ORBツリーとローカルな八分木ツリーの組み合わせとなる。この実装では、ローカルなツリーを作るとのは同じで、そのプロセッサに属する粒子と相互作用する粒子とセルのリストを作り、それをローカルなツリーに追加するというアイデアを採用している。これにより、個々のプロセッサの持つツリーはほぼ最適となる(ORB+ローカルツリーでは、幾何学的に近い粒子が別のノードに割り当てられてしまう)。
Gadget-2 (Springel 2005)
| BD | Oct-Tree + Mesh |
| DD | Peano-Hilbert ordering |
| P | TreePM |
Gadget-2は、Gadget-1の後継であるが、実装の詳細は大きく変わっている。この業界のスタンダードなコード。TreePM法とは、重力のような長距離力を、短距離成分と長距離成分に分離して、それぞれを別の重力ソルバーで解く手法であり、名前が表すとおり、短距離にはツリーを、長距離にはPM法特にFFTベースでPoisson方程式を解く。この方法は本質的にはParticle-Particle Particle-Mesh(PPPM)の拡張であり、短距離成分の計算をツリーで加速するということがポイントになる。なおTreePM法自体はSpringelの提案ではなく、Xu 1995によって提案された。Gadget-2ではより精密化された定式化によるSPHを採用しているだけでなく、SPHと組み合わせた多相星間物質のモデルや、星形成モデル、冷却関数等々、様々な物理過程も含んでいる。N体シミュレーションで最も大規模な計算のひとつはGadget-2(の特殊な最適化バージョン)でおこなわれた。TreePM法なので、周期境界条件はPMの部分をFFTで解くことで、自然と満たされている。
PPPM and TreePM Methods on GRAPE Systems (Yoshikawa & Fukushige 2005)
| BD | Oct-Tree + Mesh |
| DD | Slab |
| P | TreePM |
GRAPE用に最適化されたTreePMコード。TreePMでは、短距離成分の計算はカットオフをもったようなカーネルによる和に帰着するので、ほとんどSPHの計算と変わらない。そのため、そもそもグローバルなツリーを作る必要はない。この実装では、領域分割としては1次元のslab分割を採用している。slab分割は一般的には、あまりスケーラブルではないが、この実装でslab分割を採用している理由は、個々のノードがGRAPE-6Aをもつクラスターをターゲットとしているからである。GRAPE-6Aをもつクラスターでは、ノードあたりの重力演算能力が普通のx86_64コア1つより10倍以上高速である。これは何を意味するかというと、同じ計算をするのにノード数を十分の一以下にできるということである。MPPで1024コア必要な計算を、GRAPEのクラスターであれば32ノードとかで実現できる。その意味では、GRAPEやGPUのような加速演算装置を持ったクラスターは、必要なMPIプロセスの数を減らすことができるので、並列ツリー法には適したアーキテクチャといえる。この論文は、ノード数が数十であれば、PMのメッシュ数が512以上もあれば、slab分割であっても十分活用できることを示している。
GreeM (Ishiyama, Fukushige & Makino 2009)
| BD | Oct-Tree + Mesh |
| DD | Extended ORB |
| P | TreePM |
Yoshikawa&Fukushige(2005, YF)のTreePMコードに、Makino(2004, M)提案のツリー法を組み合わせたもの。M2004, YF2005ともに、GRAPEと組み合わせたツリーコードであるが、GreeMはGRAPEボードをターゲットとはしていない。国立天文台のCRAY XT-4をターゲットとして開発された(のだろう)。そのため、ノードあたりの演算性能が落ちるため、YF2005とは異なり、領域分割はORBベースのものに変更されている。ただし、GRAPEの代わりに、Nitadori(2006)による、SSE2を利用した高速なGRAPE互換x86_64プロセッサ用ライブラリPhantomを利用している。Phantomを使うことで、1コアあたりの重力演算性能として10 - 30 Gflopsを得ることができる。CRAY XT-4では、NP = 1024コアまでよくスケーリングしていて、これはGadget-2よりもよい。
京コンピュータ用に最適化されたバージョンで2012年のGordon Bell Prize(Ishiyama, Nitadori & Makino)を受賞した。
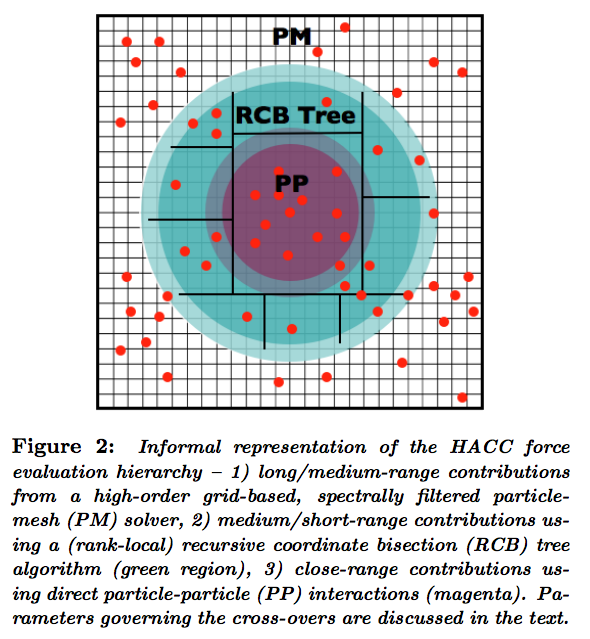
HACC (Habib etal. 2012/2013)
| BD | |
| DD | |
| P | Multi Level TreePM |
2012年のGB prizeにて、GreeM(京)と直接対決(BlueGeneQ)して、敗退したコード。 2013年もGB filnalistであったが、残念ながら再び受賞を逃している。
2HOT : Improved Parallel Hashed Oct-Tree (Warren 2013)
| BD | Morton key and Hash based Oct-tree |
| DD | Morton or Peano-Hilbert ordering |
| P | Locally Essential Tree(LET) |
http://dl.acm.org/citation.cfm?id=2503220
HOTが帰ってきた。熱すぎるということで。
最近流行のTreePMではなく、あくまでもツリー法にこだわり高速化している。 そのために、遠距離の成分は高次の多重極展開を利用することで効率化をはかっている。 全体的な並列化の手法は元のHOT論文からほぼ変わってはいない。 宇宙論計算に特化することで、一様密度の成分を差し引いたり、 宇宙論にあわせた積分手法を採用するなど、問題に特化した最適化が行われている。
