2012年ころから、GPUクラスターでの並列ツリーコードがいくつか発表されている。
私の関係者や知るところでは、Ogiya etal. (doi:10.1088/1742-6596/454/1/012014) と Bedorf etal. BONSAI (doi:10.1016/j.jcp.2011.12.024) がある。 二つのコードは、グローバルな並列化方針は似通っていて、Makino 2004ベースであるが、 GPUの利用方法が異なる。 Ogiyaらのコードはツリー構築はホストでおこないツリー走査と相互作用計算をGPUでおこなう (Nakasato 2011 の方法 http://dx.doi.org/10.1016/j.jocs.2011.01.006)。 それに対して、BONSAIはツリー構築、ツリー走査、相互作用計算を全てGPUでおこなう。 どちらもツリー構築のアルゴリズムはMortonキー+ソートを使っている。
以下の図はそれぞれのコードの性能を筑波大学計算科学センターのHA-PACSで評価したものである。
###Ogiya etal.のstrong scaling
N = 32Mの場合
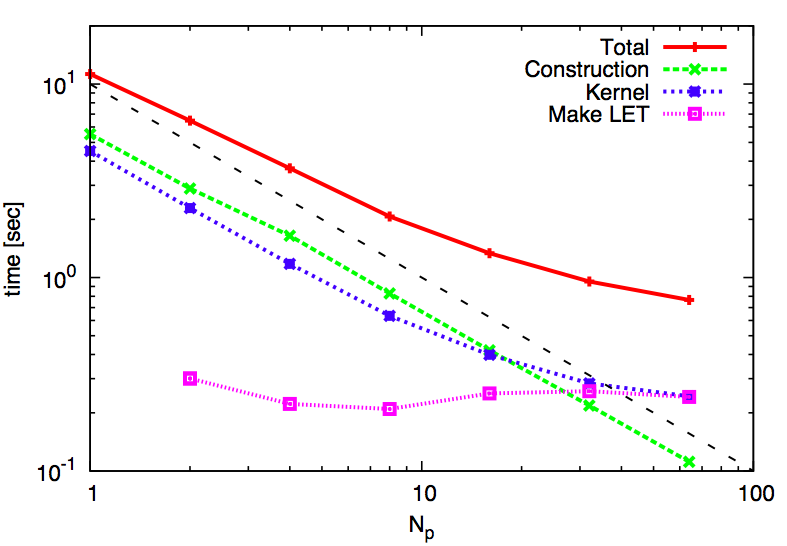
###BONSAIのstrong scaling
http://www.ccs.tsukuba.ac.jp/files/slides/sympo2013/24-fujii.pdf より
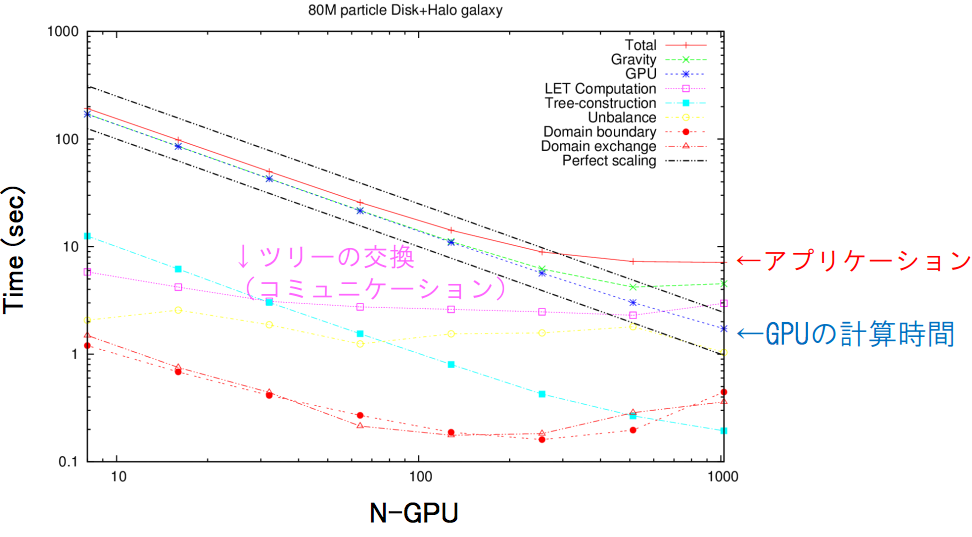
加速度の演算精度パラメータが不明であるのと、粒子分布が異なるため単純には比較できない。 どちらも、HA-PACSでGPUあたりの粒子数が多いならば、よくscalingしている。
最近、我々は(Watanabe & Nakasato HEART'14発表 プレプリント http://arxiv.org/abs/1406.6158 )、 また別の並列ツリーコードを実装し、HA-PACSで性能評価をした。 我々の手法は、PPPT法(Oshino, Funato & Makino 2011)にもとづいて、 短距離部分と長距離部分で力を分割して、それぞ別のツリーによって計算をおこなう。 元々のPPPT法は衝突系のために提案され、短距離部分は四次のHermite法で高精度に積分をし、 長距離部分はツリーを使って演算量を減らしまた時間積分も二次のLeapfrogにすることで、 トータルの計算時間を減らすことを主眼としている。 我々の方法は、計算時間を減らすと共にノード間通信量を減らすことで、 よりよいスケーリングを達成することを目的としている。 短距離部分のツリーは局所的なツリーとなるため、プロセッサ数が多い(かつ最適に領域分割されている)ならば、 近接ノード間での通信のみで更新できる。 長距離部分のツリーは全対全の通信が必要になるが、 PPPT法と同様に二つの成分毎に時間積分の頻度を変えているため、頻繁には発生しない。 これによりさらなる演算量と通信量の削減を達成できる。 GreeMなどのTreePM法と比べると、FFTで計算していたPM部分を、 独立したグローバルなLETツリーとして計算するものである。 どちらのツリー計算も、Nakasato 2011の方法でOpenCLによりGPUで加速化している。 領域分割はMakino 2004の方法であり、負荷分散はIshiyama etal. 2009の手法である。
我々のHybrid Tree法のHA-PACSでのstrong scalingの評価は以下の図になる。 ただし、これは「短距離のKickを3回、長距離+短距離のKickを1回、領域分割を1回」を1サイクルとして、 このサイクルあたりの計算時間である。通常のツリー法は毎step長距離+短距離のKickをしていることに相当する。 粒子はPlummer分布。短距離力のカーネルはDLLである。 他パラメーターがたくさんあるが、説明はとりあえず省略。

N = 32Mの時のbreakdownは以下の通り。 ただし上記の説明の通りT_total = 3*T_hard(短距離)+ T_soft(長距離+短距離) + T_DD(領域分割)である
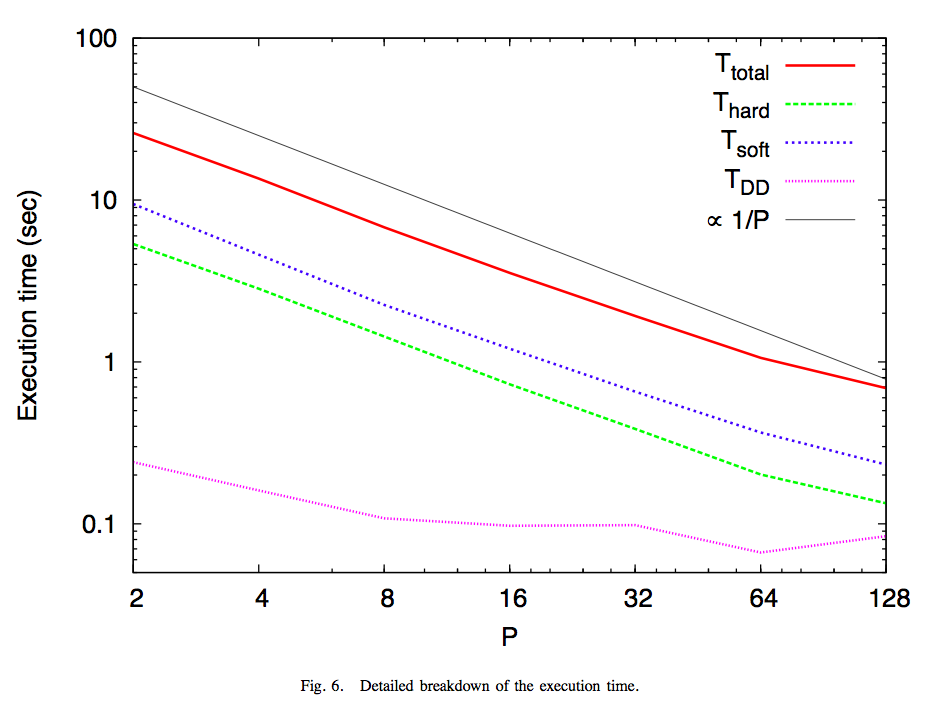
短距離部分の計算はグローバルなLETツリーの部分よりも高速であるしscalingも若干よい。 領域分割の時間がflatになってしまうのは、他のコードと同じ。 問題によっては長距離部分の計算をおこなう頻度をもっと減らしても問題ないであろう。 渡辺さんの修士論文では、それをパラメータとして、エネルギー保存を比較し、 様々な場合の比較をおこなっている。近いうちにTechnical Reportとして公開予定。