距離の計算は粒子が関わるシミュレーションでは必ず必要な演算で、それを高速化することが結構クリティカルである。伝統的なGRAPE式の演算の換算方法では、1相互作用(加速度とポテンシャル)の計算に必要な演算数を38演算としている。実際に必要な演算数を数えると、平方根を除いて20演算しかない。そのうち1つは除算であるが、平方根と除算は結果が出るまで複数サイクルかかるので、それらを10演算とすると39演算と換算できる。1演算の誤差は無視して欲しい。
この「換算」は最初のGRAPEが開発された90年代ころには、それなりに根拠のある換算であって、実際に必要なサイクル数を計測して決められている(Warren 1997)。ポイントはこの時に演算精度は指定していないことで、GRAPEが非常に効率が良く高速であった理由の1つは演算に単精度や倍精度のような標準形式を使わなかったからである。重力相互作用計算に最適に各演算に必要な演算精度を評価し、演算形式もradix 2の浮動小数点にこだわらずに、固定小数点や対数形式を組み合わせている。
2014年は最初のGRAPE-1が開発されてから25年周年とのことである。現代ではこの換算はあまりにも過大評価すぎる。いや、90年代の終わりくらいからすでにそうだったろう。それでもいまだに除算や平方根は加算や乗算のように1サイクルでは計算できないので、速く計算できるに超したことはない。逆数平方根が高速に計算できると、このような場合の除算を省略できるし、単位ベクトルの計算にも便利であるので、x86の命令には12ビット精度で逆数平方根をかえす命令が追加されている。より精度が必要であれば、それを初期値としてニュートン収束を適用すればよい。
そのような命令が追加される前、PCゲームの世界では有名なトリックがあった。
Lomont 2003より

この”magic number”の謎についてはWikipedia http://en.wikipedia.org/wiki/Fast_inverse_square_root の記事が詳しい。さらには逆数平方根についての学位論文(学部) Robertson 2012 http://shelfflag.com/rsqrt.pdf があるとは! 起源を調べるとPCのゲームではなく、1986年のdraft論文までさかのぼることができるらしい。
http://www.netlib.org/fdlibm/e_sqrt.c
このソースコードのコメント部分に、シフトと整数加算で平方根/逆数平方根が約8bit精度で得られるとある(draftの著者はあのIEEE standard 754のKahanとK.C.Ng)。このコメントの”magic number”(逆数平方根)は0x5fe80000である。上の数字と少し違う。というのもこの”magic number”は必ずしも最適ではないからだ。
上記Wikipedia記事から参照されているLomont 2003とMcEniry 2007は、最適な”magic number”を見つける手法についてまとめている。どちらも浮動小数点フォーマットの説明からはじめて、なぜ2つの整数演算で逆数平方根が得られるのかを証明したうえで、誤差評価をおこない、最適な値を計算機で検索するという方法を使っている。後者のほうがより一般性があり詳しい。結果、得られた最適な”magic number”は0x5f375a86 or 0x5f375a85であるそうだ。Lomontの方法で前者が計算され(x86と関係あるんですかねぇ…)、McEniryはそれに加えて85でも同じくほぼ最適であるとした。Robertson 2012は、McEniryや他の仕事を参照して、0x5f375a86が最適値であることの証明をしている。
さらに、2014年のblog記事 http://multigrad.blogspot.jp/2014/04/math-evolution-and-dirty-tricks.html では、遺伝的プログラミングを使ってこの数字を発見しようと試みている。しかも、”magic number”だけではなく、組み合わせる整数演算もパラメータとして、遺伝的プログラミングで探索・最適化してみたという。結果は0x5f33f870。得られた数式は”(a+a) - (x >> 1)“だそうだ。惜しい。
| ソース | 年 | magic number | double |
|---|---|---|---|
| Kahan & Ng | < 1986 | 0x5fe80000 | |
| Quake 3 | < 2002? | 0x5f3759df | |
| Lomont | 2003 | 0x5f375a86 | 0x5fe6ec85e7de30da |
| McEniry | 2007 | 0x5f375a85 | 0x5fe6eb50c7b537aa |
| Robertson | 2012 | 0x5f375a86 | 0x5fe6eb50c7b537a9 |
| Multigrad | 2014 | 0x5f33f870 |
得られる演算精度は約8bitだから、符号部指数部とつなぐと1+8+7(hidden bitを除いて) = 16bitになり、数値シミュレーションのようにそのあとにニュートン収束を使うことが前提ならば、一番最初の”0x5fe80000”で実は十分である。Quake 3などのゲーム用CGで、単位ベクトルの計算等に使うのであれば8bit精度の中で最適なほうがよいのだろう。
2009年の最近の話題 http://www.geocities.jp/andosprocinfo/wadai09/20090314.htm エントリによると、HPC-ACEでは8 bit精度の逆数平方根(と逆数)、PowerISA V2.06では5 bit精度の命令が追加されている。とすると、テーブルを使うまでもなく、この方法を使っているのかもしれない。一応、1e-12から1e12の間の全ての単精度変数について、誤差の頻度分布を計算してみた(単精度変数を網羅してテストする手法の参考: http://randomascii.wordpress.com/2014/01/27/theres-only-four-billion-floatsso-test-them-all/ )。ただし、引き算は上位16bitだけ。”Newton N”はニュートン収束をN回したもの。SSE2のrsqrtps命令は比較のために。
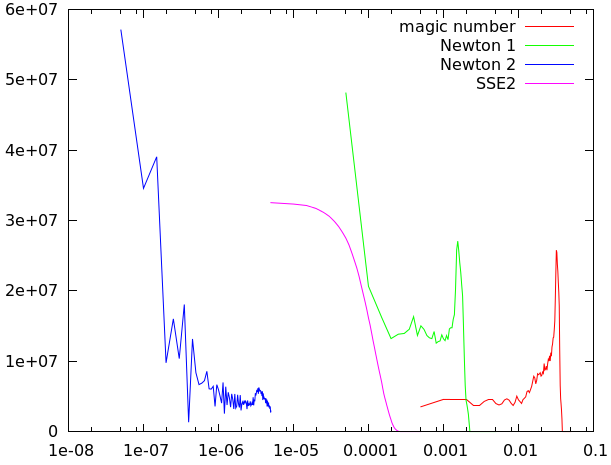
rsqrtps命令と比べると、誤差の頻度分布は変な形をしている。ニュートン収束を2回してもまだ完全に単精度にはならない。単精度でニュートン収束が3回以上必要だとすると、なんということでしょう、「GRAPE換算」よりサイクルがかかってしまうではありませんか。biasも心配ではあるし、安全を取るならば5bitでもテーブルを使った近似なのかなあ。
なおGRAPEシリーズでの平方根と除算の取り扱いは世代によって異なる。最初のGRAPE-1は、そもそも全ての演算がROM化されていたので、平方根もROMをひくだけだったろう。その後継である低精度バージョンのGRAPE-3やGRAPE-5は、入出力は整数でパイプライン途中は対数形式の浮動小数点を採用していて、この場合平方根は1bitシフトするだけという夢のような高速化が可能であった。一方いわゆる高精度なGRAPE-2にはじまる偶数シリーズは、世代ごとに詳細が異なるし全てを把握しているわけではないが、基本的には内部は通常の浮動小数点演算形式のため、テーブル補間をベースにしたものであろう。分子動力学用のMD-GRAPEシリーズは、距離を引数とした任意のテーブルを設定することができるので、明示的に平方根は計算していないと思う(要確認)。最後に、我々が設計した高精度演算でプログラマブルなGRAPE-MP( http://dx.doi.org/10.1016/j.procs.2011.04.093 )は、128 bit浮動小数点演算をハードとして実装しているが、加算器乗算器に加えて単精度相当の逆数平方根のユニットを持つ。これに採用したのは2次のチェビシフ補間である。この場合三回ニュートン収束すると必要な精度が得られる。